Recursos, recursos y ... más recursos

Está claro que en Internet hay de todo y para todos, los recursos que se pueden encontrar sobre matemáticas son muy variados y realmente copiosos en información. La permanencia de los mismos depende en gran medida de un soporte humano que se encuentra tras bastidores, recopilando, verificando y catalogando la información que se va a montar, y también debe contar con recursos técnicos y económicos que garanticen su disponibilidad. Cada vez es más frecuente que las empresas de software presten servicios de soporte y publiquen recursos gratuitos para cualquier usuario interesado en buscarlos y usarlos; esta es una buena manera de garantizar que si hoy publico un enlace sobre recursos de matemáticas, física, álgebra, entre otros, ese mismo enlace se encuentre vigente por mucho tiempo (así no tendré que estar pendiente de eliminar la entrada por haber sido eliminado el contenido del enlace ¿cierto?).Como sea, la empresa VAXA SOFTWARE  es una de esas compañías que dedican tiempo y recursos humanos y económicos para montar un repositorio de material bastante atractivo y sugerente, tanto para docente como para estudiantes, de muy variadas áreas relacionadas con la madre de las ciencias (y con esto no me refiero precisamente al ocultismo ni la astrología). Revisen pues este enlace que no tiene desperdicio, algún día (cuando alguien por fin lea este blog) me lo agradecerán. A continuación en enlace:

VAXA - Recursos Educativos Gratis

Imprimir tu propio papel para graficar

Imagina esta situación: Pasada la media noche, veinte o cuarenta ejercicios  (¿quién lleva la cuenta?) de cálculo de áreas en coordenadas polares; vas por el próximo y de pronto te das cuenta que... ya no tienes papel para graficar. En este caso tienes tres opciones: irte a la cama (que sería lo más sensato a estas alturas), tratar de graficar sobre alguna de las otras gráficas que tienes regadas por el piso de tu estudio... o puedes googlear "papel polar"  y ver que pasa. De nuevo la gente de Google salva el día y pone a tu disposición 339.000 entradas relacionadas con el papel polar. De todas éstas me quedé con la primera de la lista (ver enlace al final de esta entrada), que me permite imprimir, no sólo mi propio papel polar, sino otros 8 tipos de papel para graficar, de los cuales, debo confesarlo, sólo conocía 4. La interfaz de entrada te permite escoger entre 8 tipos de papel a imprimir:

1. Papel en escala de coordenadas Cartesianas 
2. Papel de Ingeniería (Que a mi se me da muy parecido al papel milimetrado vulgar común y corriente)
3. Papel Polar
4. Papel en escala Isométrica
5. Papel en escala logarítmica
6. Papel en escala hexagonal
7. Papel de gráfica de probabilidades
8. Carta de Smith

También puedes seleccionar entre pulgadas y milímetros como unidades de medida para las escalas, el tamaño del papel (Carta o A4), y otras propiedades características de cada tipo de papel.

He aquí el enlace a Print Free Graph Paper

A ver si alguien quiere comentar para que sirve cada uno de los tipos de papel disponibles en esta página o si conocen otro sitio similar a éste para imprimir papel para graficar. Toda colaboración es bienvenida.

Gráficas de funciones

¿Cansado de tabular a mano? ¿Cansado del papel milimetrado, el papel polar y las reglas plásticas? Bueno, no te canses mucho porque aún pasará mucho tiempo antes que se dejen de usar. Mientras tanto puedes ayudarte un poco con estas herramientas en linea para graficar funciones. No pretendo hacer un análisis de cual es mejor, así que las presento sin ningún orden en particular. 

Graficador 3D

Introduce una función como texto lineal y oprime el botón "GRAPH"

Graficador 2D

Puedes introducir hasta tres funciones y ver sus gráficas simultáneamente. Sólo introduce la ecuación en forma de texto lineal (ver el ejemplo que viene pre cargado en la página) y pulsa el botón "GRAHP"

FooPlot: Gráficas de funciones en 2D

Puedes ver las gráficas de hasta 5 funciones a la vez. Aumentar o reducir el área visible de la gráfica. Copiar y pegar la gráfica como imagen en una presentación o como código "embed" para tus páginas web.

Gráficas de funciones en 3D 

Otro graficador de funciones en 3D.  Introduce la parte explícita de la ecuación, configura la escala y los intervalos en los ejes cartesianos y pulsa en "Graph the Function!" para ver la gráfica de tu función. Si te ha fastidiado el no poder visualizar una superficie en 3D proveniente de una función de varias variables ¡ESTE ES UN BUEN MOMENTO PARA EMPEZAR!

Los tres sitios que he seleccionado, como casi cualquier otro generador de gráficas de funciones, de basan en la misma interfaz de entrada de datos. Una linea de texto donde introducir la ecuación en forma de texto lineal; así, por ejemplo, la ecuación de una parábola básica se escribiría: y=x^2, donde el usuario sólo escribe la parte de la ecuación correspondiente a la(s) variable(s) independientes, es decir, sólo se introduce la parte explícita de la función (x^2). Los demás parámetros necesarios son los intervalos a graficar en los ejes x e y, así como la escala de cada eje. Generalmente ya vienen predeterminados, pero se pueden ajustar para destacar mejor la gráfica en estudio. En resumen, se trata de tres muy buenas herramientas para graficar funciones con un aporte adicional como es el poder ver como afecta cambiar los valores de las constantes en la forma de la gráfica en tiempo real. Esto resulta particularmente útil a la hora de diseñar evaluaciones. Ya, basta de cháchara y ¡¡A GRAFICAR!!

Museo de Matemáticas

Museo Interactivo de Matemáticas

Échenle un ojo  a este nuevo y curioso museo, ubicado en Manhattan,  que promete reunir gente y esfuerzos para la divulgación y una mejor comprensión de las Mates y sus aplicaciones. Una de las mayores trabas que se presentan en un curso de Mates es demostrar sus aplicaciones y sus variantes. Este museo hace hace de la interactividad su herramienta principal en la demostración de teoremas para llegar a personas de todas las edades y sin necesidad de conocimientos previos o profundos de matemáticas. Me recuerda un poco al Museo de los Niños, en Caracas, dedicado a lo mismo pero orientado a todas las ciencias en general. También hacían un muy buen uso de la interactividad. 

Más información sobre este museo en su página oficial http://momath.org/

Respuestas insólitas 2:

Primer semestre de ingeniería. Primera clase de Matemática I: Siempre comienzo repasando algunos puntos básicos. La manipulación de expresiones algebraicas constituye uno de los mayores obstáculos que se encuentran los estudiantes en su primer contacto con el cálculo Superior.

Comienzo con una inocente pregunta: 

- ¿Qué resulta de sumar 1 + 2 + 3 + 4? - La respuesta y las miradas de "¿Qué le pasa a este tipo? ¿Es que nos cree retrasados o qué?" no tardan en aparecer

- ¡10! - Responden con tono cansino y puedo ver expresiones de suficiencia y de "me la estoy comiendo" por todas partes. Continúo con las preguntas inocentes.

-¿Qué resulta de sumar 2X + 3X + 5X? - Esta vez asoma algún rictus de sorpresa y duda, pero la respuesta correcta llega entre murmullos y expresiones de "¡Ah! Ya lo sabía".

- ¡10X! - Responden algunos mientras los demás guardan un silencio prudencial sin abandonar su expresión de suficiencia. Continúo mi ronda de preguntas escribiendo en la pizarra acrílica.

-¿Qué resulta de sumar...?

 

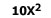– Responden, casi a coro y comienza a renacer mi esperanza en el género estudiantil y acaricio la suave sensación de un semestre de buenos resultados. 

Suelto entonces la pregunta definitiva, la que me sacará de todas las dudas. La que me demostrará si esa sensación ilusoria será o no realidad

- ¿Qué resulta de sumar... ?

 ¡Caos total! Surgen varias respuestas a la vez; discusiones sobre quien tiene la razón. Escribo todas las respuestas que me dan el la pizarra:

– dicen algunos

– alcanzo a escuchar de otros

En concreto: Ninguna respuesta correcta. Todavía trato de comprender el intrincado proceso mental que les impulsa a manipular de esa manera los exponentes y a dar esa respuesta insólita. Más aún, todavía me cuesta hacerles comprender que esa última suma es imposible, que no se puede realizar y que se debe dejar hasta allí, que no hay nada más que hacer. Como dije en mi post anterior, lo que hace tan complicado sacarlos de este error, es que ESTÁN CONVENCIDOS QUE ÉSA ES LA RESPUESTA CORRECTA. Cada quien, a su manera de ver las cosas, piensa que está en lo correcto y mientras más convencidos están, más difícil es sacarlos de su error.

Respuestas insólitas 1:

Siempre había querido  hacer una recopilación de las respuestás más insólitamente incorrectas con las que me he encontrado en los exámenes  de mates que he aplicado a lo largo de mi experienca docente, así como otras que he encontrado en algunos sitios de internet. La idea no es tomarlo en broma o ridiculizar a quienes he tenido la oportunidad de tener como alumnos, más bien es resaltar el extraño factor común que todas estas respuestas fueron escritas con el pleno convencimiento de su veracidad, es decir, quienes las escribieron estaban seguros de estar en lo correcto, con la consecuente dificultad para sacarlos de su error.

Voy a comenzar este especial con un video que muestra de una manera sumamente divertida el hecho de cómo una persona puede aferrarse a una respuesta errónea aún cuando la respuesta correcta sea evidente a nuestros ojos.

Crédito para la gente del blog No Sólo Mates (de cuya existencia apenas me entero, pero recomiendo ampliamente) en la traducción del video.

Lo más cercano al concepto de inmortalidad:

"El recuerdo de Arquímedes persistirá cuando Esquilo esté ya olvidado, porque las lenguas mueren y los conceptos matemáticos no. Inmortalidad es tal vez un término estúpido, pero quizá un matemático posea las mayores probabilidades de alcanzarla, sea cual sea su significado."

G. H. Hardy

Godfrey Harold Hardy (1877 - 1947) fue un matemático británico, mentor del matemático hindú Ramanujan (otra historia interesante sobre matemáticos brillantes de origen humilde). 

Para quienes se pregunten: ¿Qué demonios importa una triste demostración que sólo unos cuantos frikis entenderán (o simularán entender)? ¿cuál es la motivación? Bien lo dice Hardy en su cita: para, de alguna manera, alcanzar la inmortalidad. El legado de todo aquél que ha logrado escribir su nombre junto a una demostración matemática universal e irrefutable persiste aún entre nosotros y persistirá hasta el final de los tiempos.